The Kinematics of Hypermiling
or, what is your time REALLY worth?
The Kinematics of Hypermilingor, what is your time REALLY worth? |

|
Most aggressive drivers believe that their behavior and driving style saves them lots of time getting from point A to B, and is worth the extra fuel burned in the process. This attempts to analyze just how much time that works out to, and map a little theory into real-life situations that may help anyone understand the pros and cons of spirited vs. conservative driving. First, we need to make some assumptions. We'll use two identical cars with everyday performance characteristics. The aggressive driver enjoys its acceleration, a middling-to-fair 0-60 in 10 seconds. To keep those annoying inter-car gaps at a minimum while arriving at the next stop, our aspiring street-racer is also willing to decelerate from that 60 MPH in 15 seconds, just enough to keep the groceries from flying off the back seat but still deriving relatively little benefit from coasting and using the built-up kinetic energy. Our hypermiler, on the other hand, knows the drivline's efficiency curves, plays it for all it's worth, and likes taking a full 30 seconds to reach the same 60 MPH, which would be considered grandmotherly-grade anemic by today's standards. As if that wasn't different enough, she's aware of the other factors always at work against the car's forward progress -- tire rolling resistance and air resistance, primarily, but perhaps she's also driving a hybrid in which a fair portion of stopping energy can be captured by gentle regenerative braking that doesn't stress the capacity of the hybrid system to store it. In a car like a Prius, for example, the benefits of longer, gentler braking stack up even more due to efficient energy recapture, but simply trying to use the brakes less in any car will leave more of the stopping work to the other unavoidable forces already on the car. A long, well-predicted glide down to the stoplight takes this driver 45 seconds, minimizing or entirely ceasing fuel consumption as early as feasible in the game -- no point in using any more fuel to get there anyway, since momentum is a form of energy storage and all the traffic has to ultimately stop. To summarize -- I've given the aggressive driver a generous 3:1 acceleration and deceleration factor: Aggressive Conservative 0-60 accel 10 30 60-0 decel 15 45 Now, we're going to put these two drivers on the same road together and have them run the same distance. Maybe they're driving hybrids, maybe something else -- doesn't really matter. We're also making the assumption of linear acceleration and deceleration and that both drivers have the leisure and space to consistently perform as they're used to. We're making a bit of a reach by hard-limiting the top speed of both cars to 60 MPH, but also requiring that both *attain* that speed, even if just for an instant, to make calculations easier and because the emphasis of this article is on the trip-time effects of acceleration and deceleration rather than steady-state conditions. The whole debate about speed limits is for another time. The minimum trip length, therefore, is what the hypermiler manages to cover during acceleration to just 60 MPH and then deceleration right back down to 0. This chart shows her velocity profile relative to time in seconds:

taking 75 seconds to complete the run. Remember your high school physics? The distance covered by this speed profile is calculated from the integral of her speed, or the area under the velocity curves. For a right triangle, area is 0.5 (b * h) or half of what the base and height would define as a rectangle. The general formula for distance, (1/2)a(t^2) also reduces to this using the given assumptions. Our units are kept simple -- seconds on the time axis and miles per hour on the speed axis, and when multiplied together to determine area we get what I'm calling "distance units" or DU -- which is simply 1/3600 of a mile.

So our hypermiler covers (0.5)(60 * 30) + (0.5)(60 * 45) = 2250 DU or 0.625 mile over 75 seconds from stop to stop. This is used as the bounding case because the aggressive driver will do the same leg in less time, by rapidly outdistancing the hypermiler at first while coming up to 60 MPH, traveling for a while, and then cramming on the brakes at the end. We're not yet sure how long the fast car needs to stay at speed, so the length of steady-state travel is left indefinite:

But the problem now is making the AREA under the aggressive driver's curve the same as the hypermiler, since they must travel the same length of road.

Over the first 30 seconds, the aggressive driver's profile can be broken into the acceleration phase, and the remainder steady-state at 60 MPH. We can also tack the deceleration component on right afterward, but the combined area under these still isn't quite enough to complete the run: (0.5)(60 * 10) + (60 * 30) + (0.5)(60 * 15) = 1950 DU falling just shy of the stopping point by 300 distance units. From that, it's easy enough to calculate that the aggressive driver needs to travel an additional five seconds at 60 MPH before starting to decelerate, bringing his traveled distance to the same 2250 DU. So now we can draw both of these profiles and be confident that the same area exists under each:
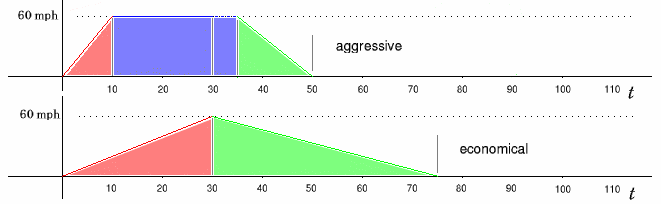
The aggressive driver lurches to a halt at 50 seconds, while the hypermiler casually drifts in at 75 seconds. The aggressive driver's 25 second lead clocks him a time advantage of 33% over the hypermiler. In fact, this time delta will *always* be 25 seconds as more length is added to the course, since when both cars are doing 60 MPH there's no additional difference in travel time other than that the zoomy one stays 10 seconds, or 1/6 of a mile, ahead of the laid-back one. (Sounds like a nice safe following distance, in fact...) We can now superimpose the speed profiles, placing the "insert point" for both cars' steady-state period of travel at the arrow. The aggressor is red, the hypermiler is (obviously) green:

and now we can begin inserting additional distance, in blue. Since we've mapped and equalized both cars' acceleration and deceleration phases as immutable sections, any added distance increases the area under both curves by the same amount -- in other words, we're just moving the stoplight farther and farther away. Here's what one full mile looks like, in which both cars remain at 60 MPH for 22.5 seconds:

which shrinks the street-racer's time advantage to 26%. As distance continues to expand, the time delta begins to have less and less significance.

Here's how it works out numerically:
| Dist | @ 60mph time |
Aggr time | Hyp time | aggr % advantage |
|---|---|---|---|---|
| 0.625 mi | (baseline) 0 | 50 | 75 | 33 |
| 1 mi | 22.5 | 72.5 | 97.5 | 26 |
| 2 mi | 82.5 | 132.5 | 157.5 | 16 |
| 3 mi | 142.5 | 192.5 | 217.5 | 11 |
| 5 mi | 262.5 | 312.5 | 337.5 | 7 |
| 10 mi | 562.5 | 612.5 | 637.5 | 4 |
And when quick-n-dirty graphed as % gain over distance traveled:
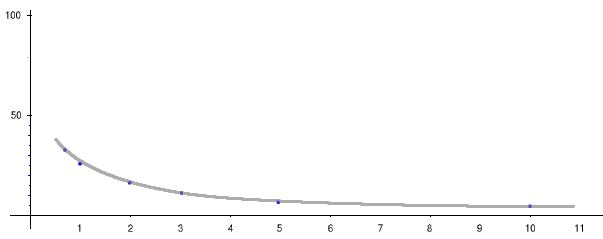
The time benefits are beginning to look fairly miniscule by comparison to the overall trip, provided that both drivers adhere to the speed limit. But wait, haven't we been reading just about everywhere that changing driving habits away from full-bore acceleration and sudden stops can easily save anyone 20% in overall fuel usage? For a trip distance greater than a mile, our supposed "time advantage" rapidly yields to the increased fuel consumption needed to attain it. Now, this is an idealized scenario for just one start/stop cycle, and real life on the roads is different -- but different in ways that over the long haul, favors the hypermiler's goals. Think of it this way: if you're looking for a challenge on the road, it is requires much more thought and finesse to calculate the energy *envelope* needed to get from here to there, as opposed to mashing a pedal to beat the other guy out of a fresh green. Now, one may immediately come up with the counterargument that the 25 seconds will make all the difference with regard to getting through the NEXT traffic light or not. Sure, an aggressive start might get the lead car to the next light before it goes yellow, but on the other hand with random light cycles, that lead car might also have to spend some time stopped at a red one -- meanwhile, the hypermiler in that long, well-predicted glide may very well reach it just as it goes green and now has some speed advantage accumulated too, and used no fuel or brake lining in the process. The aggressive driver then has to burn to *catch up* and keep going! The math starts to get gnarly from there, but suffice to say that in everyday traffic, the signals are the "great equalizer" -- without illegally running reds or being in an emergency vehicle on call, the aggressive driver has to wait just like everyone else and the perceived time savings quickly becomes just that -- a perception. There is absolutely nothing wrong with spending a large part of the "red time" in coasting TO the light, as opposed to just sitting there looking up at it. The waste heat difference is significant. Now, where do we get to go 60 MPH between lights? -- on those fairly major secondary highways, where we nonetheless have signals but the distances between them are often quite long, extending the "blue" part of the trip even longer and shrinking the relative difference. For a run on an interstate, it truly doesn't matter how fast anyone starts or stops, which every trucker who's climbed out of a mountainside rest stop knows quite well -- even if he has to crawl up that next hill at 40 MPH with the 4-ways on, the load gets where it's going on time. About the only scenario that gives the puncher-of-pedals a continuously increasing time advantage is a sequence of stop signs a couple of city blocks apart, with no cross traffic. Hops can be immediately chained together, and he'll come out of it with glowing brake rotors and an empty tank, but way ahead of the hypermiler. Fortunately, such environments only occur in certain regions of towns and are thus small and/or rare. So make your own tradeoff. 20% more fuel burned for a 4 or less percent time factor most of the time? Doesn't seem worth it, does it? And we haven't even touched on the increased safety and decreased frustration factors that the less aggressive driver routinely enjoys._H* 071030, 080325